선형회귀와 최소제곱법
두 변수를 대표할 수 있는 직선
잔차
두 변수를 대표할 수 있는 그래프를 그리기 위해서 산점도를 찍어 보면
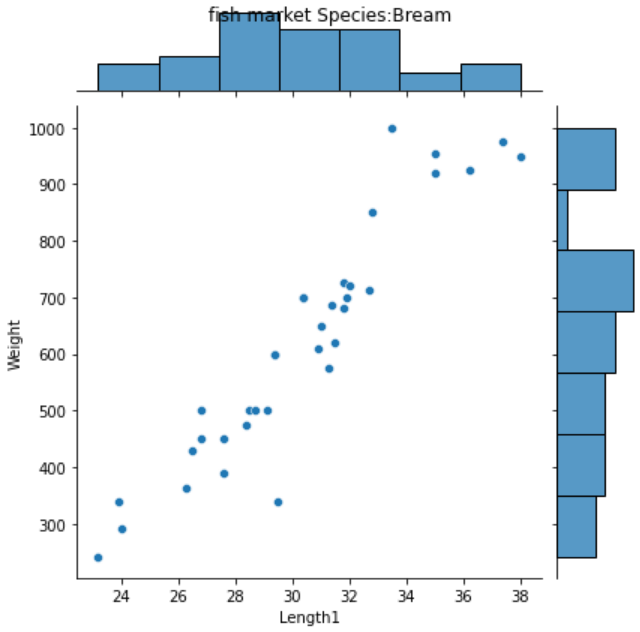
이 점들을 근사하는 직선을 생각할 수 있는데
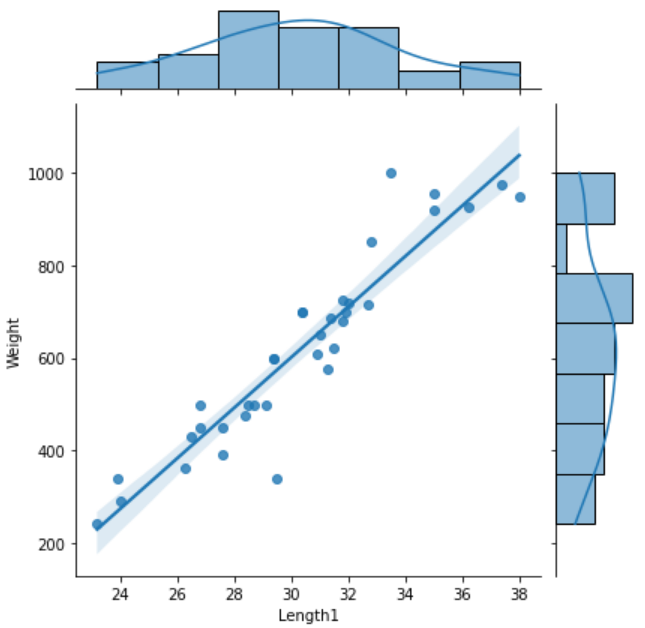
데이터들의 선형성을 대표하는 직선은 잔차를 통해 나타낸다 잔차는 해당 데이터의 y값 에서 임의의 직선 Weigint= a+b(Lenght1)의 y값을 빼서 구한다.
이 residual^2가 최소가 되게 하는 직선을 구하는 것이 최소제곱법을 통한 선형 회귀이다.
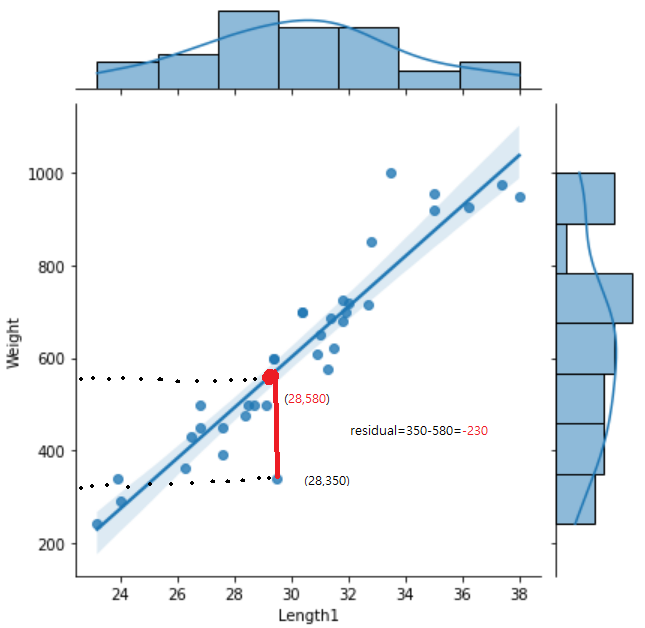
잔차의 제곱을 사용하는 이유
잔차의 합을 생각해보았을 때 큰 양의 잔차와 큰 음의 잔차가 서로 더해지면 실제로는 잔차가 큰 것임에도 불구하고 잔차가 작은 의미가 되어 버릴 수 있다.
또한 잔차의 제곱을 사용하면 잔차의 절댓값이 커질수록 제곱을 더 큰 값을 가지게 되어서 잔차가 매우 큰 이상치를 발견하는 것을 더 쉽게 만든다.
최소제곱법을 이용한 직선 구하기
위의 그래프는 아래의 도미 데이터35개를 이용한 것인데 어떤 방식으로 잔차의 제곱이 최소가 되는 직선이 만들어지는지 확인해보려고 한다.
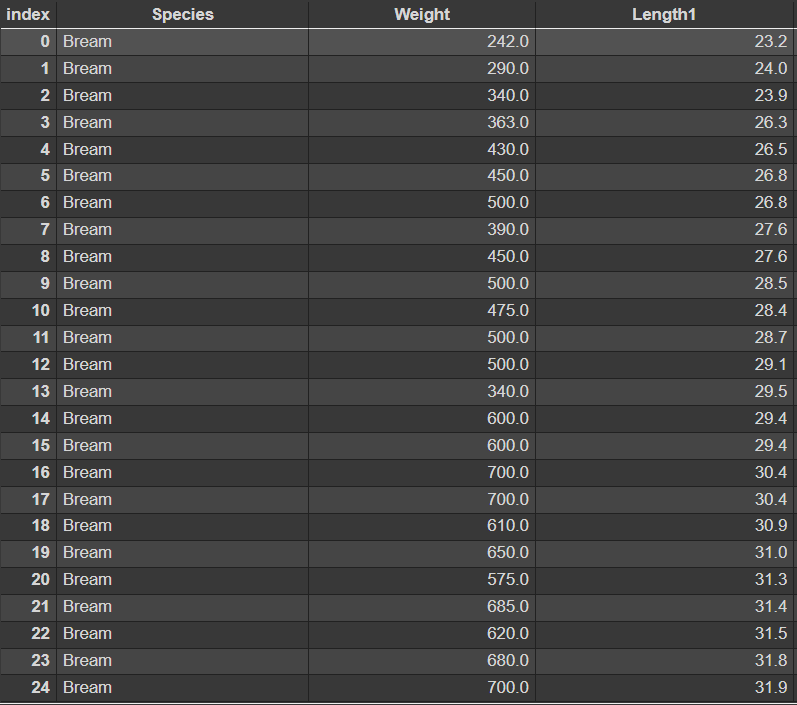
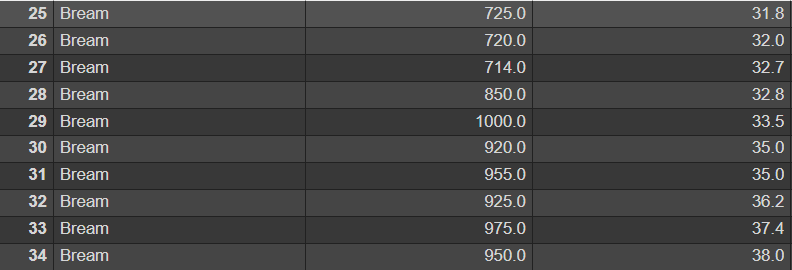
\[y_i=Weigint_i=(242,290,340..) \\
x_i=Lenght1_i=(23.2,24.0,23.9..)\]
\[Weigint= a+(Lenght1) \\
\\
242=a+b*23.2 \\
290=a+b*24.0 \\
340=a+b*23.9 \\
363=a+b*26.3 \\
...\]
\[\begin{pmatrix}
1&23.2\\1&24.0\\1&23.9\\1&26.3\\...
\end{pmatrix}
\begin{pmatrix}
a\\b
\end{pmatrix}
=
\begin{pmatrix}
242\\290\\340\\363\\...
\end{pmatrix}\]
\[간결하게 표시하면 \\
\\
Mv=y\\
\\
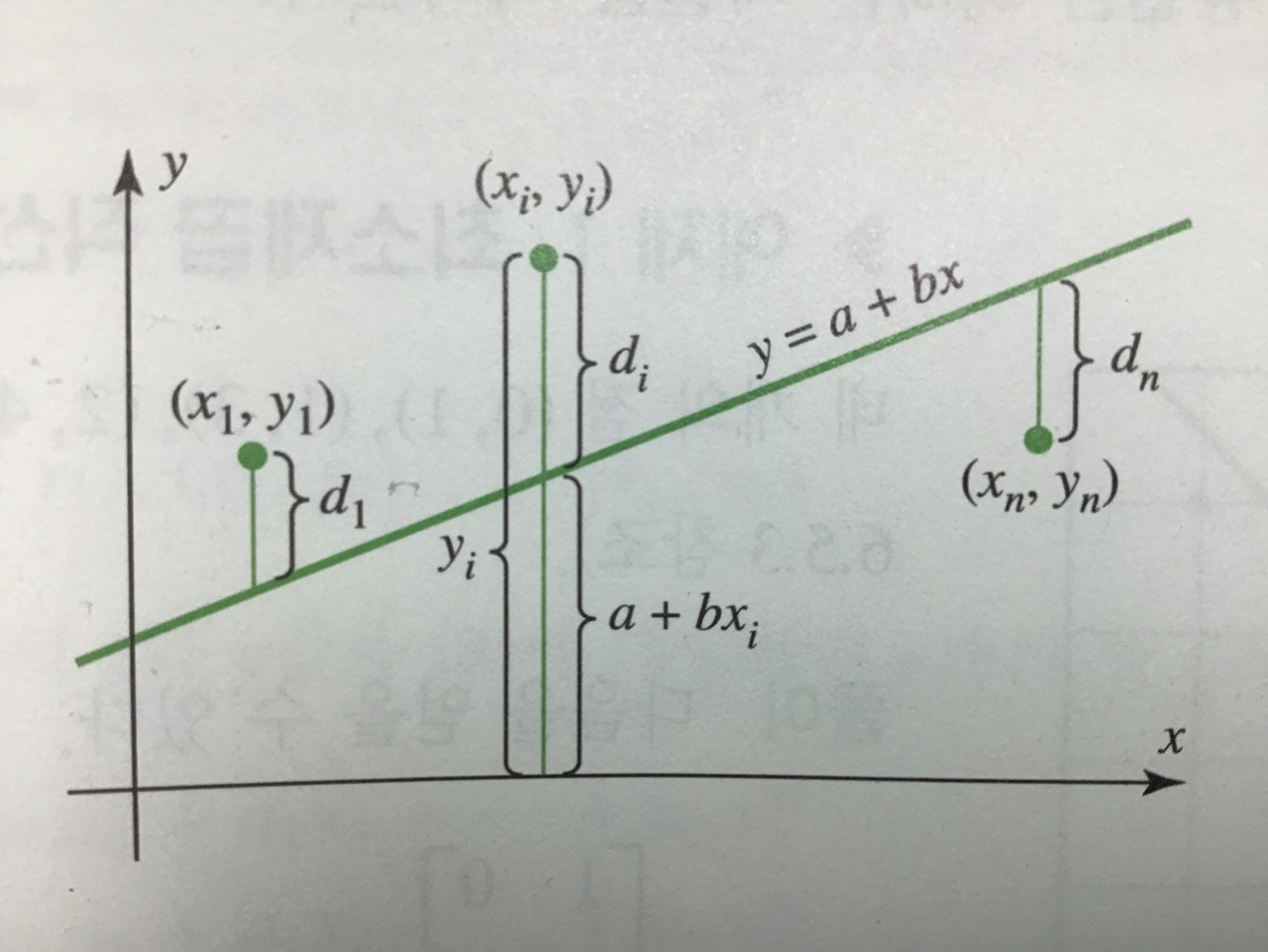
||y-Mv||^2=(y_1-a-bx_1)^2+(y_2-a-bx_2)^2+...+(y_n-a-bx_n)^2\\
d_1=|y_1-a-bx_1| 이라 놓으면\\
\\
||y-Mv||=d_1^2+d_2^2+d_3^2+...+d_n^2\]
\[Mv=y\\
\\
M=
\begin{bmatrix}
1&x_1\\1&x_2\\1&x_3\\1&x_4\\...
\end{bmatrix}
\;and \quad
y=
\begin{bmatrix}
y_1\\y_2\\y_3\\y_4\\...
\end{bmatrix}
\\
\\이라\,하면\,유일한\,최소제곱\,직선적합\\
y=a^*+b^*x
\\가\,존재한다\\
\\v^*=
\begin{bmatrix}
a^*\\b^*
\end{bmatrix}
\\
\\
정규방정식에 의해\\
Mv^*=y\\
M^TMv^*=M^Ty
\\ \\
v^*=(M^TM)^{-1}M^Ty\]
위 식을 통해서 기울기와 절편값을 구해 보면 아래의 값이 나오는데

위의 기울기와 절편으로 그린 그래프와 Seaborn의 regplot으로 회귀곡선을 그려준 것을 비교해보면
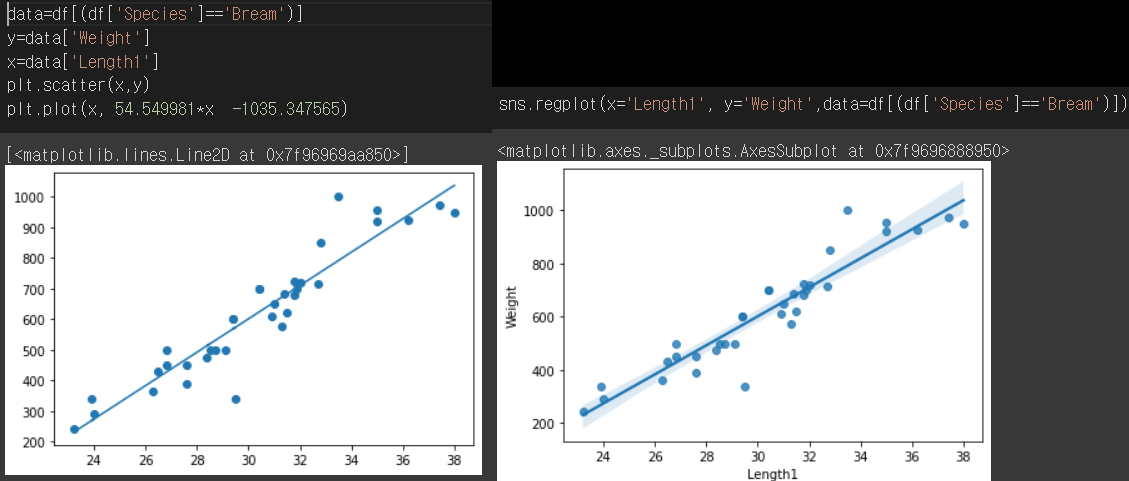
비슷한 직선이 나오는 것을 확인 할 수 있다.
참고
HOWARD ANTON, CHRIS RORRES, 알기쉬운 선형대수 개정 11판, 김태균,박미경,이호재,이희정,정정주,한광희 옮김, (주)한티에듀, 2019년, 427~430쪽







