연쇄 법칙과 역전파

연쇄 법칙 (Chain Rule)

연쇄 법칙은 함수의 합성에 대한 미분을 계산하는 규칙이다

\[만약 \ 함수 h(x)가 \ 함수 \ g(u)와 \ 함수f(x)로 \ 이루어져 \ 있다면, \ f(x)의 \ 미분은 \ 다음과 \ 같이 \ 계산된다. \\ \frac{d}{dx}h(x)=\frac{d}{du}g(x)⋅ \frac{d}{dx}f(x) \\ \\ f(x) = (x+1)^2, \ g(u) = u^3+2u−5 \ 이라면 \\ h(x) = g(f(x)) \ 이고 \\ \frac{d}{dx}f(x) = 2(x+1), \ \frac{d}{du}g(x) = 3u^2+2 \ 이므로 \\ \frac{d}{dx}h(x) = (3u^2+2)⋅(2x+2), \ u = (x^2+1) \ 을 \ 대입하면 \\ \frac{d}{dx}h(x) = (3(x+1)^2+2)⋅(2x+2) = 6x(x+1)^2 + 10(x+1)^2 = (6x+10)(x+1)^2 \ 가 된다\]

간단하게 겉미분을 적용한 수 속미분을 적용한 것과 같은 결과가 나온다

---

역전파 (Backpropagation)

위의 연쇄 법칙은 역전파에서 순서대로 미분을 적용하는 데 사용된다

예를 들어 아래와 같은 신경망이 존재한다고 가정하자

input(x)

Linear Layer(W1)

Linear Layer(W2)

Linear Layer(W3)

output(y)

• output이 어떻게 나오는지 그 과정을 살펴보면

input(x)

Linear Layer(W1)
- z1 = W1 * x + b1
- a1 = activation(z1)

Linear Layer(W2)
- z2 = W2 * a1 + b2
- a2 = activation(z2)

Linear Layer(W3)
- z3 = W3 * a2 + b3
- y = activation(z3)

output(y)

• 이렇게 계산된다고 볼 수 있다

• 예측값과 target의 차이를 구하여 손실함수를 계산한다
  • L = 손실함수값
• 역전파의 첫 번째 단계로 손실 함수 L의 기울기(dL/dy)를 구하는 과정
• Linear Layer 3 (Output Layer) 의 역전파의 과정을 살펴보자

z3 = W3 * a2 + b3
y = activation(z3)

\[손실 \ 함수 \ L을 \ 네트워크 \ 출력값 \ z3로 \ 미분한 \ 값 \ = \ \frac{dL}{dz3} \\ 손실 \ 함수 \ L을 \ 출력값 \ y로 \ 미분한 \ 값 \ = \ \frac{dL}{dy} \\ 출력값 \ y를 \ 네트워크 \ 출력값 \ z3로 \ 미분한 \ 값 \ = \ \frac{dy}{dz3} \\ \\ 연쇄 \ 법칙을 \ 사용하여 \ 값을 \ 구할 \ 수 \ 있다 \\ \frac{dL}{dz3}=\frac{dL}{dy}*\frac{dy}{dz3} \\ \\ b는 \ 편향을 \ 의미 \\ \frac{dL}{db3}=\frac{dL}{dz3}*\frac{dz3}{db3} \\ \\ W는 \ 가중치를 \ 의미 \\ \frac{dL}{dW3}=\frac{dL}{dz3}*\frac{dz3}{dW3} \\\]

예시

• forward propagation

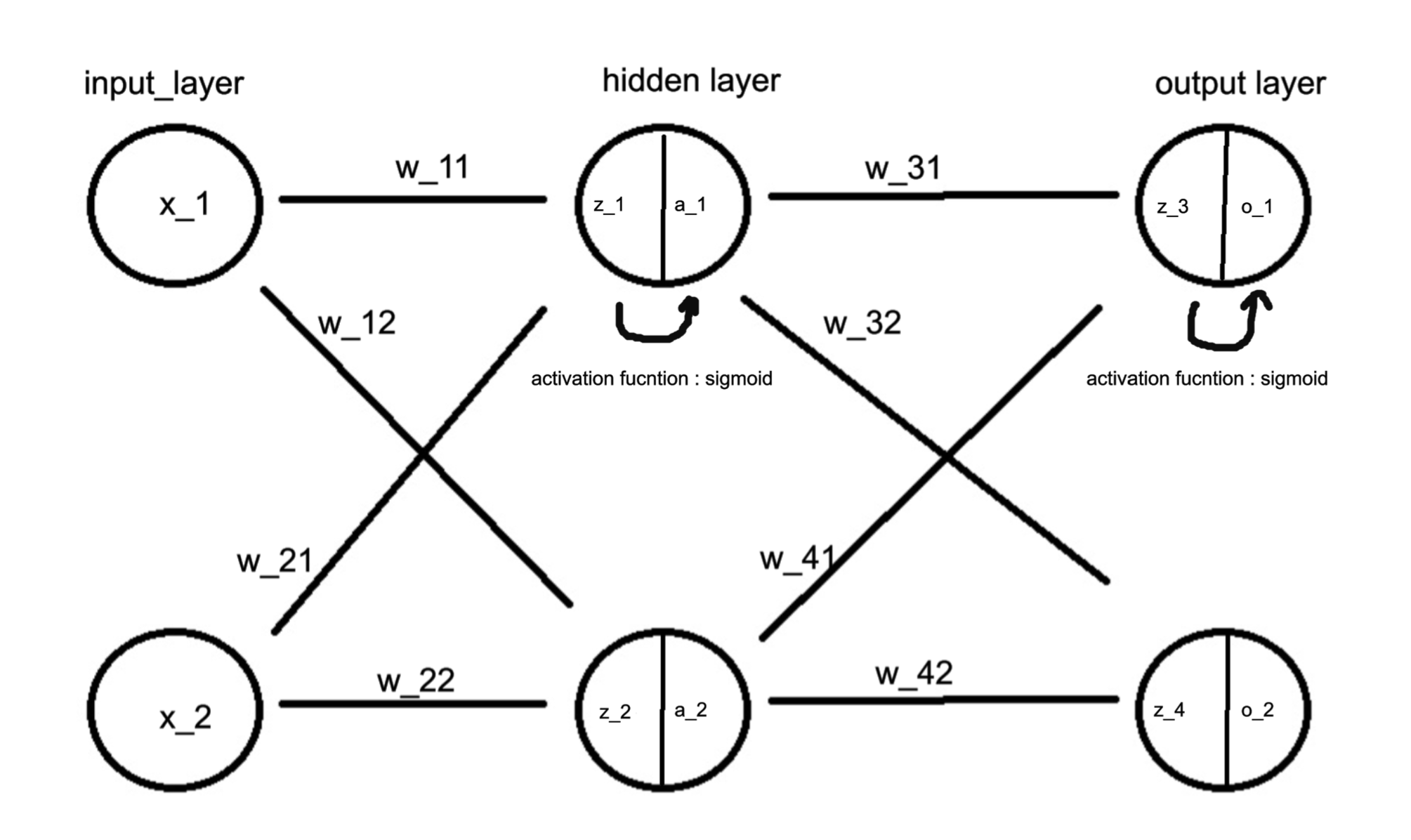
\[은닉층 \\ z_1 = w_{11} ⋅x_1+w_{21}⋅x_2+b_1 \\ z_2 = w_{12} ⋅x_1+w_{22}⋅x_2+b_1 \\ \\ a_1 = \sigma(z_1) \\ a_1 = \sigma(z_2) \\ \\ \sigma(z) = \frac{1}{1+e^{-z}}\\ \\ 출력층 \\ z_3 = w_{31} ⋅x_1+w_{41}⋅a_2+b_2 \\ z_4 = w_{32} ⋅x_1+w_{42}⋅a_2+b_2 \\ \\ o_1 = \sigma(z_3) \\ o_2 = \sigma(z_4) \\\]

• Loss function(MSE)

\[E_{o1} = \frac {1}{2}(target_{o1} - output_{o1})^2 \\ E_{o2} = \frac {1}{2}(target_{o2} - output_{o2})^2 \\ E_{total} = E_{o1} + E_{o2} \\\]

• backpropagation

\[가중치 \ 업데이트 \\ \frac{\partial E_{tortal}}{\partial W_{31}} = \frac{\partial E_{tortal}}{\partial o_{1}} ⋅\frac{\partial o_{1}}{\partial z_{3}}⋅\frac{\partial z_{3}}{\partial 2_{31}} \\ E_{tortal} = \frac {1}{2}(target_{o1} - output_{o1})^2 + \frac {1}{2}(target_{o2} - output_{o2})^2 \\ \\ \frac{\partial E_{tortal}}{\partial {o_1}} = \frac{\partial}{\partial o_1}(E_{01}+E_{o2}) = \frac{\partial E_{01}}{\partial o_1}\\ \\ ※ \ o_1 \ 로 \ 미분하기 \ 때문에 \ E_{o2}는 \ 사라진다 \\ \\ \frac{\partial E_{tortal}}{\partial {o_1}} = -(target_{o1} - output_{o1}) \\ \frac{\partial o_{1}}{\partial z_{3}} = o_1 ⋅ (1-o_1) \\ \frac{\partial z_{3}}{\partial 2_{31}} = 1 \\ \\ \\ ※ \ z_3 = w_{31}⋅x_1 +b는 \ 선형적으로 \ 의존하므로 \ 미분시 \ 1이 \ 된다 \\ \frac{\partial E_{tortal}}{\partial W_{31}} = -(target_{o1} - output_{o1})⋅o_1 ⋅ (1-o_1)⋅1 \\ W^+_{31} = w_{31} - \alpha\frac{\partial E_{tortal}}{\partial W_{31}} \\ \\ \alpha = learning \ rate\]

이와 같은 방식으로 가중치 업데이트를 계속 해 간다

reference

https://wikidocs.net/37406